AC-261 Účinky proudu blesku na svody i ve stavbách
| OTÁZKA: |
| Účinky proudu blesku na svody i ve stavbách |
|
ČSN EN 62305-3 ed. 2 v čl. 5.3.4 uvádí mimo jiné, že na svodech LPS musí být zabráněno vytvoření instalačních smyček. Pokud tomu není možno zabránit, musí být dodržena dostatečná vzdálenost mezi konci vodiče tvořících smyčku. Jako důvod, proč je nutno tuto vzdálenost dodržet, vyplývá z článku 6.3 normy (podle kterého se tato vzdálenost počítá), že je nutno při úderu blesku zabránit přeskoku mezi těmito konci. Existuje ještě nějaký další důvod, proč je třeba dodržet uvedenou vzdálenost? Jaké mohou být další účinky blesku? |
| Otázku podává: |
| ODPOVĚĎ: |
|
Kromě nebezpečí přeskoku hrozí také zatížení vodiče smyčky velkou mechanickou silou. To je ostatně známo i z teorie. Tu nebudeme podrobně rozebírat. Postačí, když se obrátíme na definici základní jednotky elektrického proudu, kterou je ampér. Zjednodušeně řečeno, jeden ampér je proud, který při průchodu dvěma přímými rovnoběžnými vodiči umístěnými 1 metr od sebe vyvolá mezi nimi stálou sílu o velikosti 2 · 10-7 (0,000 000 2) newtonu na 1 metr délky vodiče. Je to síla velice nepatrná a snad i těžko představitelná a obtížně měřitelná (přibližně je to síla, kterou by takřka mikroskopická kapička vody o průměru menším než třetina milimetru působila svou tíhou na podložku).
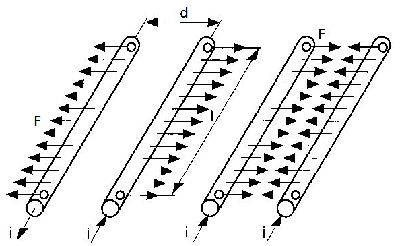
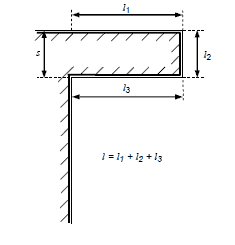
Obr. 1 Směry sil vyvolaných průchodem elektrického proudu rovnoběžnými vodiči Znalci fyziky nechť následující řádky vynechají (ty jsou určeny pouze těm, kteří mají z nesrozumitelných vzorečků z doby, kdy zasedali ve školních lavicích, přinejmenším smíšené pocity): Jestliže u jednoho vodiče zvětšíme proud 10krát (to znamená, že jím bude protékat proud 10 A), zvětší se síla mezi oběma vodiči 10násobně. Jestliže pak zvětšíme proud v druhém vodiči 10krát (to znamená, že oběma vodiči bude protékat proud 10 A), zvětší se síla mezi těmito vodiči 100násobně. Obdobně, necháme-li oběma vodiči protékat proud o intenzitě 1 000 A (což je sice značný proud, ale oproti proudům blesku to ještě nemusí nic neznamenat), pak se ta síla zvětší milionkrát, to znamená, že nabude hodnoty 0,2 N (pokud vám to ještě nic neříká, je to síla, kterou tlačí na podložku závaží dvou deka neboli 2 dkg). A podobně, když se dostaneme na hodnoty, které jako maximální (z hlediska normy nikoliv z hlediska přírody uvádí ČSN EN 62305-1 ed. 2, tj. 200 kA, tedy 200 000 A) pro LPL I, zjistíme, že souběžné vodiče, kterými (každým z nich) protéká takovýto proud, na sebe na vzdálenost 1 m působí silou 200 000 × 200 000, tj. 40 000 000 000krát větší, než síla vyvolaná průtokem proudu 1 A, tedy silou 8 000 N (což je síla rovnocenná té, kterou působí zemská tíže na závaží o hmotnosti 800 kg). Jestliže máme smyčku o celkové délce vodiče 2,2 m, přičemž délky l1 = l3 = 1 m a l2 = s = 0,2 m (viz obr. 2), to znamená, že vzdálenost vodičů se sníží na pětinu, působící síla se pětkrát zvětší. Jestliže tedy touto smyčkou protéká výše uvedený proud 200 kA, bude odpudivá síla mezi horním a spodním vodičem smyčky ještě 5krát větší, to znamená 40 000 N (tedy síla rovnocenná působení závaží 4 tun).
Obr. 2 Smyčka na svodu Pro znalce fyziky:
ve kterém: Jestliže dosadíme do výše uvedeného vzorečku příslušné veličiny, dostaneme:
Dospěli jsme tedy ke stejnému výsledku jako při uplatnění výše uvedených primitivních úvah. Pokračování: Uvedený příklad byl výjimečný. Blesky obvykle takovou energií nedisponují a proudy blesku se obvykle rozdělí do více svodů. Přesto však je možno na obr. 3 ukázat příklad toho, že k vytržení svodu při úderu blesku skutečně může dojít.
Obr. 3 Vytržení svodu v důsledku úderu blesku Uvedený příklad nám ukazuje také, proč není radno
a proto je nutné provádět na systémech ochrany před bleskem nejen pravidelné revize, ale i revize po úderu blesku. Uvedený příklad – vytržení svodu z podpěr - není jediný, který dokumentuje mechanické síly vyvolané proudy blesku. Poměrně časté jsou případy vedení elektrických rozvodů vytržených ze zdi. Blesk si hledá tu nejkratší cestu do země, a ta se často ubírá právě elektrickými vodiči, které na sebe působí velkými silami – viz obr. 4.
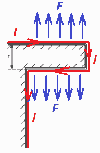
Obr. 4 Vytržení vedení elektrického rozvodu Další nebezpečí, s kterým uvažuje i norma, je nebezpečí tepelného působení na vodiče a vůbec na veškeré části, které vedou proud blesku. Opět vezměme LPL I. Pro tu se v ČSN EN 62305-1 ed. 2 (v tabulce 3) udává specifická energie (která se průchodem proudu blesku přemění v energii tepelnou) 10 MJ/W. To znamená, že když proud blesku projde vodičem, jehož odpor je 1 Ω, uvolní se v tomto vodiči uvedená energie 10 MJ a tento vodič se touto energií zahřeje. (Vzhledem k tomu, že doba průchodu proudu je velmi krátká, řádově ne větší než milisekundy, veškerá tato energie se věnuje na oteplení vodiče). O jakou teplotu se tedy touto energií ohřeje svod z pozinkované oceli o průřezu 50 mm2? Řešení: cT = (přibližně) 3,6 J.cm-3. K-1. Takže celková tepelná kapacita jednoho metru tohoto vodiče je uvedená měrná tepelná kapacita násobená objemem (v cm3) jednoho metru svodu, který je 0,5 cm2 × 100 cm = 50 cm3. Takže celková tepelná kapacita jednoho metru svodu je 3,6 J.cm-3. K-1 × 50 cm3 = 180 J. K-1. Oteplení způsobené průtokem proudu blesku pak je Δϑ = 40 000 J/180 J. K-1 = 222 K. Takže pokud byla teplota svodu před úderem blesku 30 °C, těsně po úderu blesku se svod ohřál až na 252 °C. To je skutečně abnormální případ, kdy by mohlo od blesku skutečně dojít ke vznícení snadno zápalných látek. Počítáme s ním pouze v případě, že se jedná o LPL I, a tedy i LPS I. Pro třídu LPS IV bychom počítali jenom se specifickou energií 2,5 MJ/W, takže oteplení by bylo pouze čtvrtinové, tj. cca 56 °C – svod by se ohřál na 86 °C. ČSN EN 62305-3 ed. 2 v čl. 5.3.4 uvádí, že není-li možno zajistit dodržení vzdálenosti mezi svodem a hořlavým materiálem, měl by být průřez svodů minimálně 100 mm2. V takovém případě se i pro LPL I sníží oteplení na polovinu, tj. na 111 K, takže teplota svodu při teplotě okolí 30 °C by i po úderu blesku byla “pouhých” 141 °C, a ta by zřejmě žádný hořlavý materiál za krátkou dobu, než svod vychladne, nezapálila. Ne vždy se však proud blesku ubírá kovovými vodiči. V případě že dojde k přeskoku skrz stěnu, opět se uvolňuje na jeden ohm dráhy proudu energie (např., jak je uvedeno výše, 10 MJ/Ω). Ovšem vzhledem k velmi malé vodivosti stěny mezi dvěma dobře vodivými částmi, mezi nimiž dojde ve stěně k přeskoku, je “těch ohmů” na krátké dráze proudu podstatně více než v předchozím případě, uvolněná energie na této dráze je značná. Způsobí enormní ohřátí stěny, odpaření vlhkosti z ní, výbuch páry ve stěně a rozvalení stěny, jak ukazuje obr. 5.
Obr. 5 Rozvalení stěny, kterou prošla část proudu blesku Účelem uvedených příkladů bylo ukázat, že si lze jednoduše udělat představu, co blesk v určitých případech může způsobit. To lze aplikovat i na jednotlivé konkrétní situace, s kterými je možno se v praxi setkat. |
- A TECHNICKÁ TÉMATA
- AA Ochrana před dotykem
- AB Dimenzování a jištění
- AC Ochrana před bleskem a přepětím
- AD Prostředí
- AE Vnitřní rozvody
- AF Koupelny a bazény
- AG Připojování el. zařízení
- AH Revize
- AJ Strojní zařízení
- AK El. zařízení ve zdravotnictví
- AL Značení a terminologie